Ray Marching

A ShiftForward tech talk by João Costa / @JD557
Notes about this talk
- Based on the work of Iñigo Quílez (iq/rgba)
- Code examples in Scala (CPU)
- Practical application should be implemented for GPUs
Overview
- Quick Rendering Intro
- A Simple Ray Tracer
- Distance Fields
- Distance Field Operations
- Illumination
Quick Rendering Intro
- Rasterization
- Ray Tracing*
- Ray Casting
- Path Tracing
- Ray Marching
- ...
Rasterization
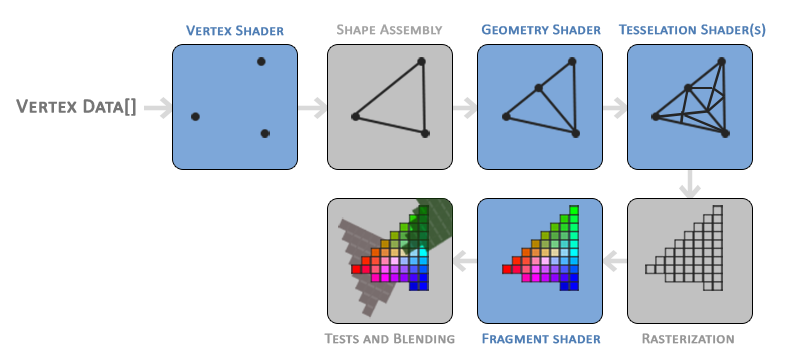
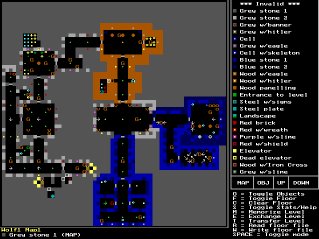
Ray Casting
- Simplest form of ray tracing
- Cast a ray for each pixel (or vertical scanline) of the image plane
- Solve ray-surface intersection test

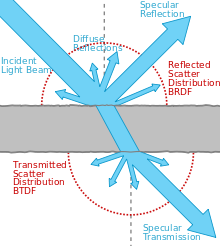
Path tracing
- Solve the rendering equation via Monte-Carlo integration
- Trace a rays with weighted random reflections/transmissions
- Multiple iterations are required to avoid noisy images

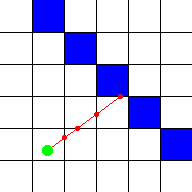
Ray marching
- Also known as sphere marching
- Objects and scenes are represented as distance fields
- Resulting image is calculated by marching through the distance field
A simple ray tracer
Object: collision function $f:R^3 \rightarrow Boolean$
eg.: $sphere(x, y, z) = \sqrt{x^2 + y^2 + z^2} \leq 1$
case class Vec3d(x: Double, y: Double, z: Double) { ... }
type Object3d = Vec3d => Boolean
val sphere: Object3d =
(v: Vec3d) => sqrt(v.x*v.x + v.y*v.y + v.z*v.z) <= 1.0
- Trace a ray from the eye to each pixel of the image plane
- "March" through it in small $\vec \Delta$ of size $\epsilon$
- If it hits someting, render a color
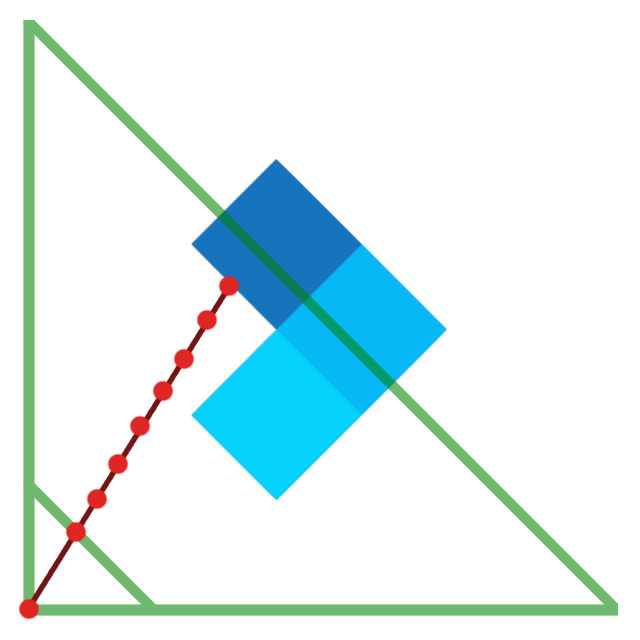
Note: this is not ray marching
def traceRay(x: Double, y: Double, obj: Object3d, eps: Double) = {
val initVector = Vec3d(x, y, zNear)
val delta = initVector.normalize
def traceRayAux(pos: Vec3d): Color = obj(pos) match {
case true =>
Color(255, 255, 255)
case false =>
if (pos.z > zFar) Color(0, 0, 0)
else traceRayAux(pos + delta*eps)
}
traceRayAux(initVector)
}
Colors and textures
Colors/3d textures can be easilly implemented:
type Object3d = Vec3d => Option[Color]
This will be ommited in this talk, as it adds unnecessary complexity to most examples.
Limitations
- Small $\epsilon$:
- Slow to converge
- Large $\epsilon$:
- Small objects can be skipped
- Objects will have "dents"
Distance fields
Object: signed distance function of a point to its surface $sdf:R^3 \rightarrow R$
eg.: $sphere(x, y, z) = \sqrt{x^2 + y^2 + z^2} - 1$
case class Vec3d(x: Double, y: Double, z: Double) { ... }
type DistanceField = Vec3d => Double
val sphere: DistanceField =
(v: Vec3d) => sqrt(v.x*v.x + v.y*v.y + v.z*v.z) - 1.0

- $sdf(\vec p)$ is the distance to the closest object to $\vec p$
- Therefore, $sdf(\vec p)$ is always a safe value for $\left | \vec\Delta \right |$
- In practice, the $\left | \vec\Delta \right | = max(sdf(p), \epsilon)$
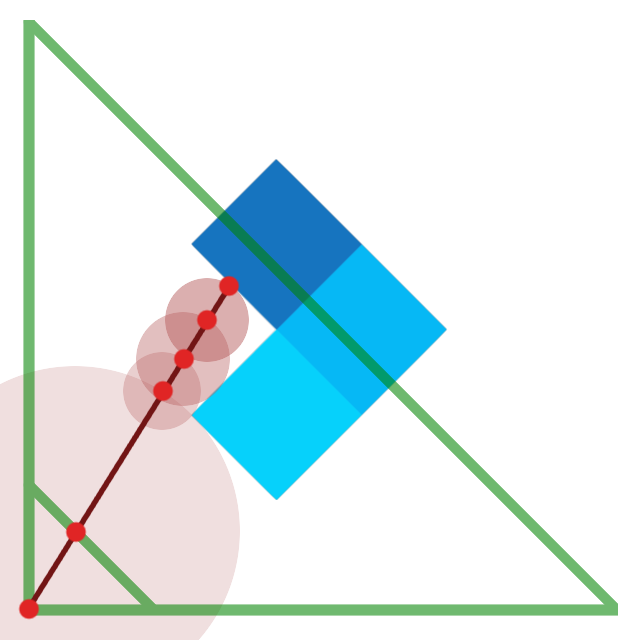
def traceRay(x: Double, y: Double, sdf: DistanceField, eps: Double) = {
val initVector = Vec3d(x, y, zNear)
val delta = initVector.normalize
def traceRayAux(pos: Vec3d): Color = sdf(pos) match {
case dist if dist <= 0 =>
Color(255, 255, 255)
case dist =>
if (pos.z > zFar) Color(0, 0, 0)
else traceRayAux(pos + delta*max(dist, eps))
}
traceRayAux(initVector)
}


$Color(r,g,b) = (iterations \times 5, 50, 50)$
Distance Field Operations
- By manipulating distance fields, we can implement:
- Boolean operations
- Geometric transformations
- Crazy stuff
Boolean Operations
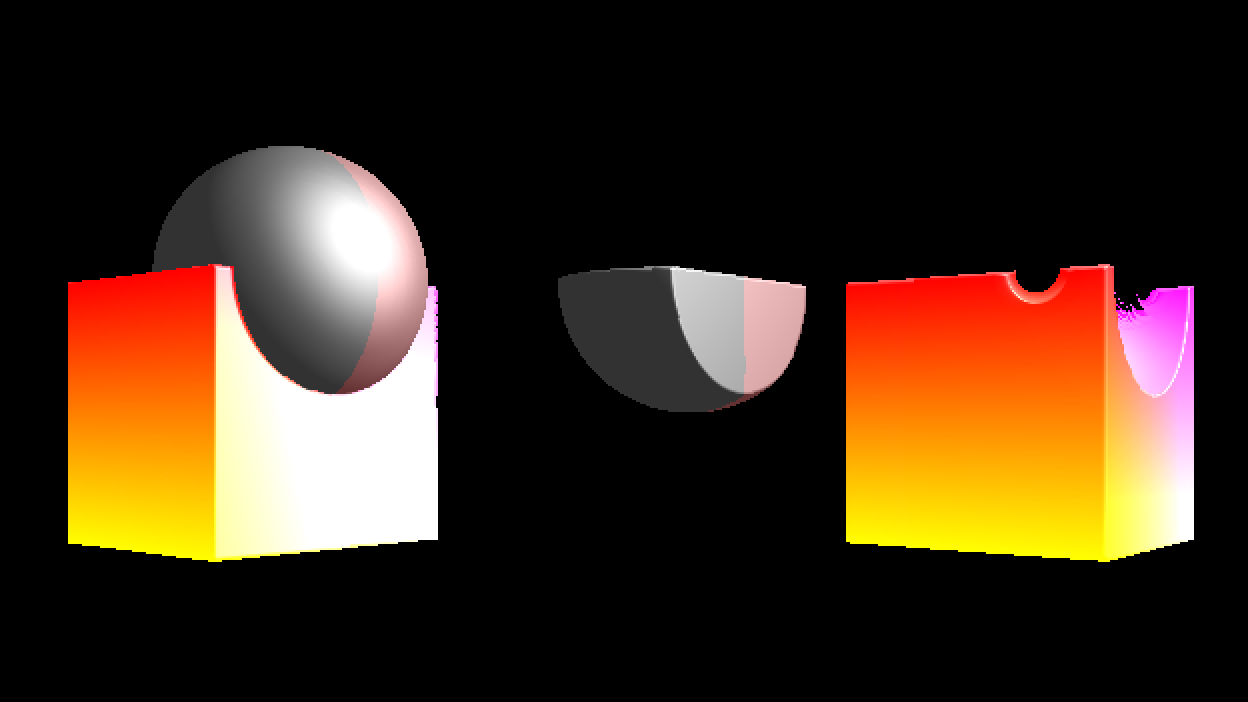
Boolean Operations
Union
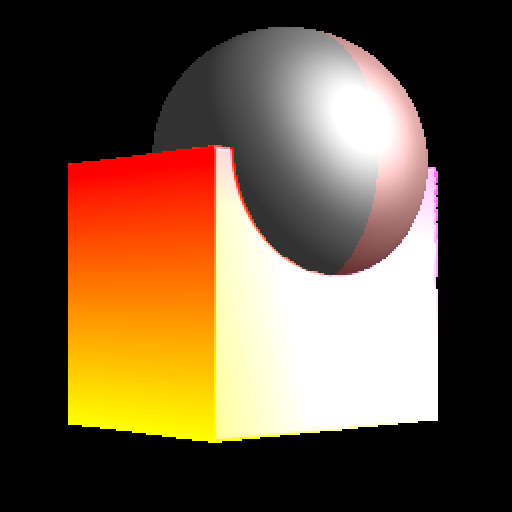 $$ obj_1 \cup obj_2 = min(sdf_1(\vec p), sdf_2(\vec p)) $$
$$ obj_1 \cup obj_2 = min(sdf_1(\vec p), sdf_2(\vec p)) $$
Boolean Operations
Intersection
 $$ obj_1 \cap obj_2 = max(sdf_1(\vec p), sdf_2(\vec p)) $$
$$ obj_1 \cap obj_2 = max(sdf_1(\vec p), sdf_2(\vec p)) $$
Boolean Operations
Difference
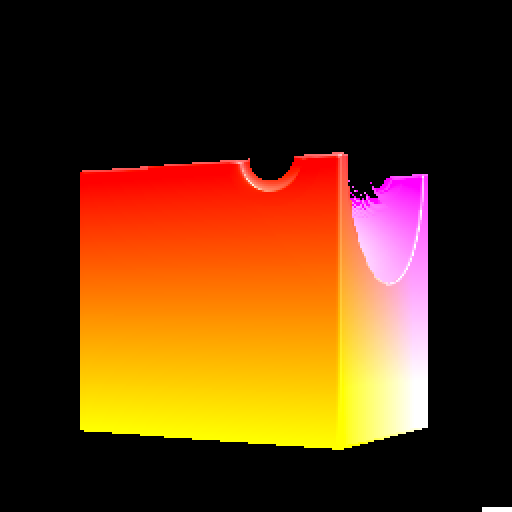 $$ obj_1 - obj_2 = obj_1 \cap (\neg obj_2) = max(sdf_1(\vec p), -sdf_2(\vec p)) $$
$$ obj_1 - obj_2 = obj_1 \cap (\neg obj_2) = max(sdf_1(\vec p), -sdf_2(\vec p)) $$
Geometric Transformations
- Translation
- Rotation
- Scale
Geometric Transformations
Translation/Rotation
- Moving objects is hard
- Moving our ray is easy
- Apply $T$ to objects $=$ Apply $T^{-1}$ to rays
Geometric Transformations
Translation/Rotation
def translate(delta: Vec3d)(sdf: DistanceField): DistanceField =
(v: Vec3d) => sdf(v - delta)
def rotateX(theta: Double)(sdf: DistanceField): DistanceField =
(v: Vec3d) => sdf(v.rotX(-theta))
def rotateY(theta: Double)(sdf: DistanceField): DistanceField =
(v: Vec3d) => sdf(v.rotY(-theta))
def rotateZ(theta: Double)(sdf: DistanceField): DistanceField =
(v: Vec3d) => sdf(v.rotZ(-theta))
Geometric Transformations
Scaling
- The same trick applies to scaling
- However, scaling a distance field will also scale our distances
- Rescale the returned distance to know how much to march
Geometric Transformations
Scaling
def scale(s: Double)(sdf: DistanceField): DistanceField =
(v: Vec3d) => sdf(v / s) * s
Crazy stuff
- We assumed that $sdf$ is continuous and exact
- We can break the rules (slightly) to obtain cool effects:
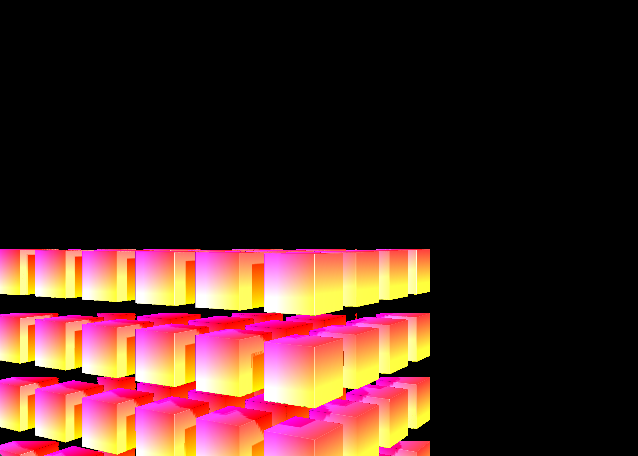
- Modulo operations: Infinite repetition
- Rotations with variable $\theta$: Twist
- Union with smooth min: Blend

Illumination
A simple illumination model: $$ ambient + \sum_L shadow_L (diffuse_L + specular_L) $$

- Global:
- $ ambient = occlusion \times K_{ambient} $
- For each light $L$:
- $ shadow_L $
- $ diffuse_L = L_{diffuse} \times K_{diffuse} \times max(\vec{N} \cdot \vec{L}, 0) $
- $ specular_L = L_{specular} \times K_{specular} \times max(\vec{R} \cdot \vec{V}, 0)^\alpha $
- How to calculate the normal vector
- How to calculate the ambient occlusion
- How to calculate shadowed areas
Normals
$\vec{N} = \nabla sdf = \left (\frac{\partial sdf}{\partial x}, \frac{\partial sdf}{\partial y}, \frac{\partial sdf}{\partial z} \right )$
def normal(p: Vec3d, scene: DistanceField, eps: Double): Vec3d = {
val dx = scene(p + (eps, 0, 0)) - scene(p - (eps, 0, 0))
val dy = scene(p + (0, eps, 0)) - scene(p - (0, eps, 0))
val dz = scene(p + (0, 0, eps)) - scene(p - (0, 0, eps))
new Vec3d(dx, dy, dz).normalized
}
Ambient Occlusion
- Constant ambient light: naïve appoximation to global illumination
- Intuition:
- Open areas should be well lit
- Small confined spaces should be dark
- Idea:
- If an object is on an open area: $sdf(\vec p + \vec N \times \epsilon) \approx \epsilon$
- If an object is on an closed area: $sdf(\vec p + \vec N \times \epsilon) \approx 0$
Ambient Occlusion
- Solution: for a point $\vec p$:
- Probe $N$ (eg. 6) points $\vec{p'_i} = \vec p + (\vec N \times \epsilon \times i)$
- Combine the real distance and the expected distance with a "magic formula", eg.: $$occlusion = 1 - \frac{\sum_i^N 2^{-i}(\epsilon \times i - sdf(p'_i))}{\sum_i^N 2^{-i} (\epsilon \times i)}$$
Ambient Occlusion
Ambient Occlusion
def ambientOcclusion(p: Vec3d, n: Vec3d, scene: DistanceField,
epsilon: Double, iter: Int) = {
val bias = scene(p)
def occlusionAux(i: Int, accum: Double, total: Double): Double =
i match {
case 0 => accum / total
case i =>
val expected = bias + (i * epsilon)
val real = scene(p + n * (i * epsilon))
val decay = pow(2, i)
occlusionAux(i-1,
accum+(expected-real)/decay, total+expected/decay)
}
1 - occlusionAux(iter, 0, 0)
}
Ambient Occlusion


Shadows
- Simple: Send shadow feelers using ray marching!
- Trace a ray from the object towards the light
- If it hits something, it's shadowed
- If it reaches the light, it's not
Shadows
Soft-shadows
- Soft-shadows: combine the $N$ distances with a "magic formula"
- Some properties about this formula
- Small distances should lead to darker shadows (min function)
- The heuristic should be disabled on the first few points:
- Avoids artifacts (the ray will start close to the object)
- We still need to consider collisions
- Shadows should get smoother with the distance
Shadows
def shadow(p: Vec3d, lPos: Vec3d, sdf: DistanceField, eps: Double, k: Int) = {
val init = (lPos - p).normalized
def shadowAux(delta: Vec3d, acc: Double): Double =
if (delta.size > (lPos - p).size) acc
else
if (sdf(p + delta) <= 0.0) 0.0
else if (delta.size * k <= 1.0)
shadowAux(delta + init * max(sdf(p + delta), eps), acc)
else
shadowAux(delta + init * max(sdf(p + delta), eps),
min(acc, k * dist / delta.size))
shadowAux(initVector * eps, 1.0)
}
Shadows


Final Result

The end
